Anyone who has a dice can play a simple game. Choose a number greater than 6. Then roll the dice until the sum of the rolled numbers is equal to or greater than the chosen number. If the sum at some point is equal to the chosen number, you win. What is the number that gives you the highest chance of winning? Mathematicians know the answer, but I have decided to develop a simple program to test it.
The dragon game
Recently, I watched a Numberphile video about evil numbers. I recommend it. If you want to learn more about the subject, watch it. But if won't, don't worry, I will try to explain you the rules here.
You have a dice - a standard one with 6 sides.
You pick a number greater than 6. For example 15.
Now, you roll the dice one by one multiple times and add the results together until the result is equal to or greater than the picked number.
For example:
roll 1 - you rolled 3. Total sum = 3.
roll 2 - you rolled 5. Total sum = 8.
roll 3 - you rolled 1. Total sum = 9.
roll 4 - you rolled 4. Total sum = 13.
roll 5 - you rolled 2. Total sum = 15. You win - the total sum is equal to the number you picked at the beginning.
The question is - choosing what number gives you the highest chance of winning?
The program to find the distribution
I quickly developed a program in Java to find the probabilities. You can find it on GitHub.
The core class is DistributionGenerator.
package com.dbapresents.randomnumssum.distribution;
import com.dbapresents.randomnumssum.dice.Dice;
import java.security.NoSuchAlgorithmException;
public class DistributionGenerator {
public Distribution testDice(int sides, int rolls) throws NoSuchAlgorithmException {
Dice dice = new Dice(sides);
Distribution distribution = new Distribution(sides);
for (int roll = 0; roll < rolls; roll++) {
distribution.increment(dice.roll());
}
return distribution;
}
public Distribution computeSumDistribution(int sides, int games) throws NoSuchAlgorithmException {
Dice dice = new Dice(sides);
int maxSum = sides * 10;
Distribution distribution = new Distribution(maxSum);
for (int game = 0; game < games; game++) {
play(maxSum, distribution, dice);
}
return distribution;
}
private void play(int maxSum, Distribution distribution, Dice dice) {
int sum = 0;
while (sum < maxSum) {
int rollResult = dice.roll();
sum += rollResult;
if (sum <= maxSum) {
distribution.increment(sum);
}
}
}
}
There are two public methods:
testDice, which builds a distribution of simple dice rolling multiple times. It is just to check the dice is close to random.computeSumDistribution, which plays the rolling game multiple times to build a distribution of a rolling total.
The dice is implemented using SecureRandom to generate pseudo-random numbers.
public class Dice {
private final SecureRandom rand;
private final int sidesNum;
public Dice(int sidesNum) throws NoSuchAlgorithmException {
this.sidesNum = sidesNum;
this.rand = SecureRandom.getInstanceStrong();
}
public int roll() {
return rand.nextInt(sidesNum) + 1;
}
}
The Distribution class has the following structure.
package com.dbapresents.randomnumssum.distribution;
import java.math.BigDecimal;
import java.math.RoundingMode;
import java.util.Arrays;
public class Distribution {
private static final int SCALE = 2;
private final int[] counts;
public Distribution(int buckets) {
this.counts = new int[buckets];
}
public void increment(int bucketNum) {
counts[bucketNum - 1]++;
}
@Override
public String toString() {
int totalCounts = Arrays.stream(counts).sum();
StringBuilder builder = new StringBuilder();
builder.append("Distribution:").append("\n");
for (int id = 0; id < counts.length; id++) {
BigDecimal perc = BigDecimal.valueOf(counts[id] * 100L, SCALE).divide(BigDecimal.valueOf(totalCounts, SCALE), RoundingMode.HALF_DOWN);
builder.append(id + 1).append(";").append(counts[id]).append(";")
.append(perc).append("%").append("\n");
}
return builder.toString();
}
}
Test the dice
The pseudo-random numbers generator is good enough, because when I print a distribution for a 6-sided dice
DistributionGenerator distributionGenerator = new DistributionGenerator();
Distribution distribution = distributionGenerator.testDice(6, 10000);
System.out.println(distribution);
I get quite even probabilities:
Distribution:
1;1665;16.65%
2;1725;17.25%
3;1653;16.53%
4;1599;15.99%
5;1678;16.78%
6;1680;16.80%
I think we are ready to play the game.
Dragon game with 6-sided dice
To generate distribution and get consistent results, I simulate playing the game 1 million times, but running this code:
DistributionGenerator distributionGenerator = new DistributionGenerator();
Distribution distribution = distributionGenerator.computeSumDistribution(6, 1000000);
System.out.println(distribution);
The printed distribution is long, and analyzing it is easier on a chart, so here it is.
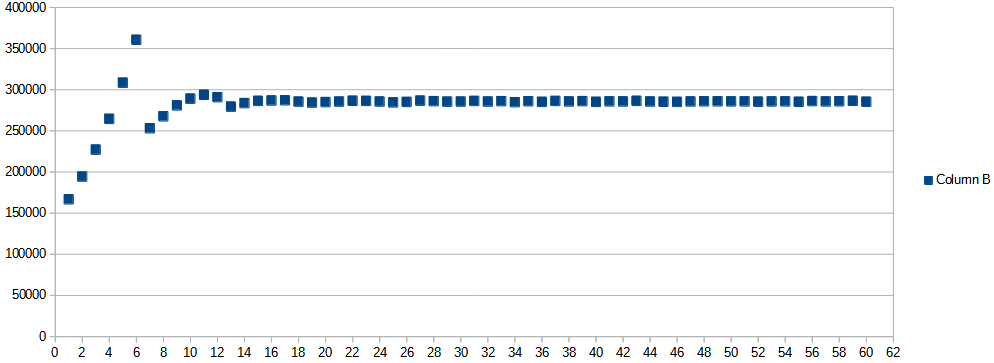
The probability in the range of 1-6 grows rapidly along with the total. That seems reasonable because the total 2 can be achieved only in 2 ways:
- 1 + 1 = 2
- 2 = 2
But the total 6 has many more possibilities:
- 1 + 1 + 1 + 1 + 1 + 1 = 6
- 1 + 1 + 1 + 1+ 2 = 6
- 1 + 1 + 2 + 2 = 6
- ...
That is why in this game you cannot choose a number from the 1-6 range, it would be too obvious.
In the totals greater than 6. The highest probability is achieved at number 11. So it is wise to choose that number in the game. But notice, that although it is the most probable, it does not have a significant advantage over other numbers.
Dragon game with 20-sided dice
How about a game with non-standard dice? For example one with 20 sides?
That is easy to check. I have to only modify a single parameter in calling the distribution generator.
DistributionGenerator distributionGenerator = new DistributionGenerator();
Distribution distribution = distributionGenerator.computeSumDistribution(20, 1000000);
System.out.println(distribution);
Here is what distribution I get:
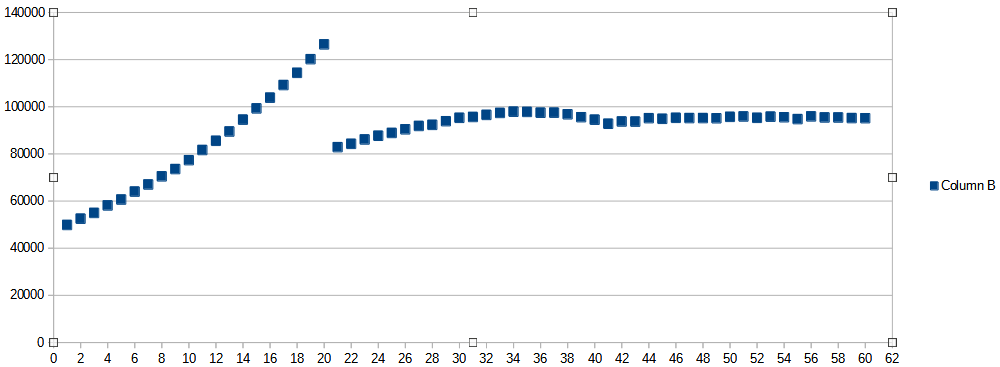
As previously, the highest probability falls on the total that is equal to the number of dice sides - 20. But that is trivial. What about the bigger numbers? It is uneasy to say by looking at the chart above as the differences are very small. So I zoom on the Y axis:
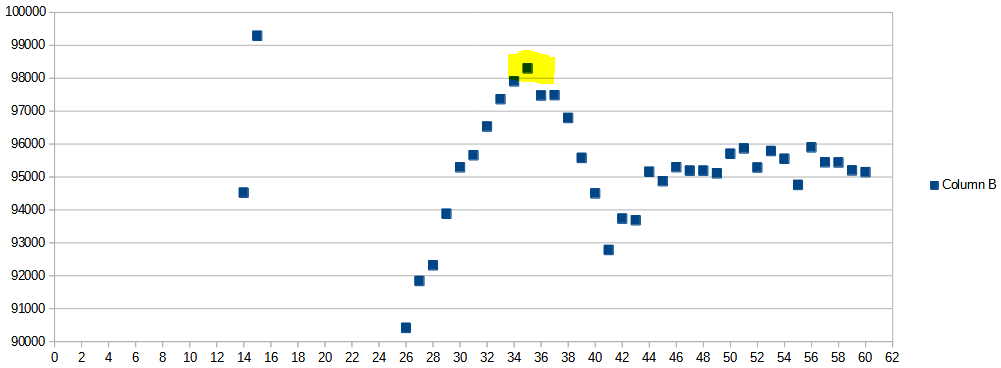
Now, we see that the number 35 has the highest probability.
If you want to play with the parameters, go ahead and download the source code from GitHub and experiment. You may also change the random number generator to see how it affects the results.


